Andrej Karpathy’s code and videos are so awesome! I love how concise his code is. His minGPT repo was an important inspiration for my “The Art of Transformer Programming” book.
Anyway, I just finished watching his BPE video and got inspired again. Karpathy’s code is really nice (as always), and his implementation is obviously not meant to be fast, but, we should be able to make the code much faster without sacrificing clarity too much. Hopefully, faster code can make experimentation (e.g. with different scores, instead of always taking the most popular pair) easier.
You can find my late night take on a minimal, clean, and fast BPE implementation here.
For his tests, Andrej used a snapshot of the Wikipedia article on Taylor Swift with ~185K chars. On my laptop, training/tokenizing this file with a vocab size of 10K takes:
| minbpe | fast_minbpe | |
|---|---|---|
| Training | 110 secs | 1.00 secs |
| Tokenization | 191 secs | 0.52 secs |
So, in this setup, we get 100X faster training.
Training fast_minbpe on the same text but with a GPT-4-sized vocab of 100K tokens takes only slightly longer at 1.61 secs, but results in a single token. Training fast_minbpe on a GPT-4-sized 100K vocab on the English translation of Marcel Proust’s “Swann’s Way”, which is the first volume of the world’s longest novel, (you can find the file, which contains just over 1 million bytes here) takes just 8.15 seconds.
This was a really fun puzzle and, as usual, I recommend trying to solve this yourself!
Below I detail the main ideas behind my implementation, and you can find the code on github.
You really should watch Andrej’s video (or at least make sure you are familiar with the byte pair encoding algorithm) before reading on.
Why is minbpe slow?
If we are to perform $N$ merges, and the length of the training text is $L$, Karpathy’s original impl does (I think):
for i in range(N):
calc_stats() # O(L)
find_max() # O(L)
do_merges() # O(L)
For a total complexity of $O(NL)$ (maybe I’m neglecting some factors).
Why is fast_minbpe fast?
So fast_minbpe does something like this:
stats = calc_stats() # O(L)
for i in range(N):
find_max() # O(log(L))
do_merges_and_update_stats() # O(M_i)
Where $M_i$ denotes the actual number of merges we perform at the $i$th iteration. Note that $M_1 + M_2 + \dots + M_n \le L - 1$, so the overall complexity of everything (again neglecting logarithmic factors) is $O(L)$!
Doing the wrong thing
The “right thing” to do here would have been to profile Andrej’s code and measure which parts take time before attempting to optimize anything. In Python btw, this can be done with a few of lines and the builtin cProfile module:
import cProfile
import pstats
from pstats import SortKey
cProfile.run('func_to_profile()', 'pstats')
p = pstats.Stats('pstats')
p.strip_dirs().sort_stats(SortKey.CUMULATIVE).print_stats(10)
p.strip_dirs().sort_stats(SortKey.TIME).print_stats(10)
Since I did this just for fun, as a quick late night exercise though, I did not do that at all. Instead, I made a quick draft of the above complexity calculations and designed a couple of data structures implementing them. I wish I had run profiling before starting (for one, I would have had more cool numbers to report). In my original implementation I actually kept the cute find_max() one-liner with the $O(L)$ complexity, and got only a 10X speedup vs minbpe, but it was not until I made the find_max() operation take logarithmic time that I got the full improvement factors above. Tl;dr - when optimizing code you should really use a profiler, but, when dealing with large objects, complexity is never wrong.
Another very wrong thing that I did is that I basically didn’t write any tests… My code produces identical outputs to Karpathy’s code (when I force both to break ties in the same way). Again - this was just a late night fun exercise :)
Laziness Pays Off
Before we dive into the implementation, I want to make a general note on lazy data structures. By saying that a data structure is lazy I mostly mean that it only does work when it is actually needed, not ahead of time. Laziness is very often a good strategy for data structures, and will indeed turn out beneficial for both the data structures we’ll use in fast_minbpe. As my good friend Danny Lumen likes to say:
“When dealing with data structures, being lazy is often the best strategy”
- Danny Lumen
Ok, let’s consider the main data structures that I used.
IndexedList
When merging, we need to delete items from the middle of our list. A simple linked list makes this efficient. We also need to know what to iterate on - i.e. we need to efficiently find all nodes containing (the first element of) a given pair. To handle that, we’ll hold a simple python dict (the index) mapping each pair to a plain python list containing the nodes from our linked list that contain the first element of the pair. Unfortunately, updating this list is hard and inefficient. Luckily, it costs us the same to update the list and to just check that it’s still up to date when accessing it, so we’ll opt for the latter solution. Yep - being lazy pays off! To remind ourselves that the index could be stale, we name it stale_index.
You can find the implementation of the IndexedList here.
Multiset
I also needed a multiset class to hold the stats. The builtin collections.Counter class is exactly the API that I needed, but its most_common function running in linear time is too slow for our purposes. Instead, I wanted to hold all the elements in a version of a max-heap that supports increasing/decreasing counts of internal elements.
You can find my implementation of Multiset here.
Note that a tiny change here made a huge difference in performance - specifically, breaking count ties explicitly i.e. doing something like this:
class Multiset:
class Node:
def __lt__(self, other):
return (self.count, self.val, self.pos) < (other.count, other.val, other.pos)
is drastically slower than breaking ties lazily like so:
class Multiset:
class Node:
def __lt__(self, other):
return self.count < other.count
as the former requires the heap to update much more (and less importantly, creating and comparing tuples is slow). This is a different type of laziness as the one I mentioned above, but it pays off as well :)
Another important change (the right kind of lazy!) was accumulating modifications and only updating the heap once a query is performed (laziness FTW!).
Putting it all together
Armed with an IndexedList and our Multiset, it’s trivial to implement the merge function, at the center of the BPE algorithm:
def merge(pair, new_id, indexed_list: IndexedList, stats:Multiset=None):
for node in indexed_list.stale_index[pair]:
if node.val != pair[0] or node.next is None or node.next.val != pair[1]:
continue # The index was stale - continue.
# Say we're merging "bc" to "X" in "abcd", and the node we're visiting now is "b".
if stats is not None: # Update the stats.
stats.remove(pair) # Remove "bc".
if node.next.next is not None:
stats.remove((node.next.val, node.next.next.val)) # Remove "cd".
stats.add((new_id, node.next.next.val)) # Add "Xd".
if node.prev is not None:
stats.remove((node.prev.val, pair[0])) # Remove "ab".
stats.add((node.prev.val, new_id)) # Add "aX".
node.next.delete() # Delete "c", we now have "abd".
node.val = new_id # Update "b" to "X", we now have "aXd".
indexed_list.update_index(node) # Add "aX" and "Xd" to the index.
Note that importantly, we are careful to skip a pair from the index if it no longer holds the desired value.
You can find my implementation here, but, as always, I recommend attempting this yourself first!
Alternatives
If you’re only interested in fast_minbpe.py feel free to skip everything below this point!
Heapy, HeapHeapHoory, and HeapyKiYay
I actually implemented the Multiset 3 times: the first version (Heapy) was fast, but a bit convoluted, the second version (HeapHeapHooray) was tiny but slower, and final implementation (HeapyKiYay) is the one I ended up using.
Version 1 - Heapy
Since I needed each element of the heap to be aware of its own position (so I could maintain the heap condition when it increases/decreases), my first attempt consisted of writing a less standard pointer-based implementation (heaps are almost always implemented in an array). You can find this impl here.
Version 2 - HeapHeapHooray
Here I decided to optimize for code length. To make this super short, I wanted to reuse the standard implementation from the heapq module.
The main idea was to create a custom list object that tells its elements where they are (so I called it a GPSList…).
Here’s the full implementation:
import heapq
class GPSList(list):
# A list-like class that tells its elements where they are:
# >>> l = GPSList(lambda i, x: print(f'{x} is in position {i}'))
# >>> l.append(3)
# 3 is in position 0
# >>> l[0] = 5
# 5 in in position 0
# We only support the subset of list operations that are needed for our heap.
def __init__(self, update_fn):
super().__init__()
self.update_fn = update_fn
def __setitem__(self, i, x):
super().__setitem__(i, x)
self.update_fn(i, x)
def append(self, x):
super().append(x)
self.update_fn(len(self) - 1, x)
# Forbid other methods that can add elements - hope I didn't forget anything :)
extend = insert = remove = __iadd__ = None
class HeapHeapHooray:
def __init__(self):
def setpos(i, x):
x[-1] = i # Our elements are lists of length 3 (count, pair, pos).
self.l = GPSList(setpos)
@property
def max(self):
return self.l[0][1]
def increase(self, x):
x[0] += 1
heapq._siftdown_max(self.l, 0, x[-1])
def decrease(self, x):
x[0] -= 1
heapq._siftup_max(self.l, x[-1])
def insert(self, val):
x = [0, val, -1]
self.l.append(x)
self.increase(x)
return x
def delete(self, x):
last = self.l.pop()
if x is last: return
if self.l:
self.l[x[-1]] = last
if x < last:
heapq._siftdown_max(self.l, 0, last[-1])
else:
heapq._siftup_max(self.l, last[-1])
This implementation is really short, but has two big downsides:
- It uses some internal functions of the
heapqmodule, so might break at some point. - It was around 5X slower than the lengthier version (but still MUCH faster than the built-in
collections.Counter!).
Version 3 - HeapyKiYay
I suspected a big reason for version 2 being slow was the custom list. My final version was based on the previous one, but consisted of getting rid of GPSList and the use of the internal heapq functions, and instead, I wrote a custom version of an array-based position-aware heap. This version is clean and efficient, so I kept it. It’s the one on github.
The Leap
I also experimented with a variant where instead of using the more custom IndexedList, I created a more general data structure (the Leap) and used it to hold the consecutive pairs directly (instead of individual tokens). I ended up preferring the code with the IndexedList so I reverted the Leap, but it is more general and might be helpful elsewhere, so I’m explaining it here.
I needed a data structure that can represent an ordered array, supporting almost the same ops as a basic doubly-linked list in O(1):
append(x): appends x to the end.delete(n): removes node n.start(x): returns the first node.end(x): returns the last node.next(n): returns the node following node n.prev(n): returns the node preceding node n.
I say almost because the leap importantly trades a list’s insert with an append operation (i.e. we can only insert at the end). In return, we get all of the following operations, in O(1) as well:
first(x): returns the first node with value x.last(x): returns the last node with value x.leap(n): returns first node after node n with the same value as n.leapback(n): returns last node before node n with the same value as n.set_value(n, x): set the value of node n to x, keeping its position (n must be the last node with value x).
In addition to standard efficient in-order iteration on all elements, a leap also allows efficient in-order iteration on all elements with a given value.
I guess that this data structure must exist, but I haven’t heard of it. So I named it - “Leap” (although maybe “Leaped List” sounds better?). Either way, if this is a thing and you know its name, please lmk!
The implementation of a leap is straightforward - you can find it here.
My first implementation of a leap was around 2X shorter (by unifying the shared logic for positions and values), but that turned out to also be around 2X slower, so I opted for the more verbose version above. Note that the shorter impl also generalizes easily to the case where we want to leap by any one of several object properties. If you’re interested, here’s the more compact and general (but slower) version:
class LinkedList: # A simple linked list.
def __init__(self, val):
self.val = val
self.prev = self.next = None
def delete(self):
if self.prev is not None:
self.prev.next = self.next
if self.next is not None:
self.next.prev = self.prev
self.next = self.prev = None # Not actually needed.
def append(self, next):
self.next, next.prev = next, self
POSITION_OBJECT = object()
class Leap:
class Node: # A leap-node is a superposition of two linked-list nodes.
def __init__(self, val):
self.val = val
self.lls = [LinkedList(self) for _ in range('pos', 'val')]
def next(self, val=POSITION_OBJECT):
return self.ll(val).next.val if self.ll(val).next is not None else None
def prev(self, val=POSITION_OBJECT):
return self.ll(val).prev.val if self.ll(val).prev is not None else None
def ll(self, val):
return self.lls[0] if val is POSITION_OBJECT else self.lls[1]
def __init__(self, init=None):
self.first = {} # Map from a value to its first occurrence.
self.last = {} # Map from a value to its last occurrence.
if init is not None:
for x in init:
self.append(x)
def nodes(self, val=POSITION_OBJECT):
node = self.first.get(val, None)
while node is not None:
yield node
node = node.next(val)
return res
def _delete(self, node, val):
# This deletes the node from just one of its linked lists.
if self.first[val] is node:
self.first[val] = node.next(val)
if self.last[val] is node:
self.last[val] = node.prev(val)
node.ll(val).delete()
def delete(self, node):
self._delete(node, POSITION_OBJECT)
self._delete(node, node.val)
def _append(self, node, val):
# This appends the node to just one linked list.
if val not in self.first: # First item with value 'val'.
self.first[val] = node
else:
self.last[val].ll(val).append(node.ll(val))
self.last[val] = node
def append(self, val):
node = Leap.Node(val)
self._append(node, POSITION_OBJECT)
self._append(node, val)
def set_value(self, node, new_val):
# Replaces the value of a node in-place.
self._delete(node, node.val)
node.val = new_val
self._append(node, node.val)
If you ever want to debug a leap, you could use something like this:
def debug_repr(leap):
p = []
for n in leap:
s = str(n.val)
if n is leap.first[n.val]: s += 'F'
if n is leap.last[n.val]: s += 'L'
p.append(s)
return '[' + ', '.join(p) + ']'
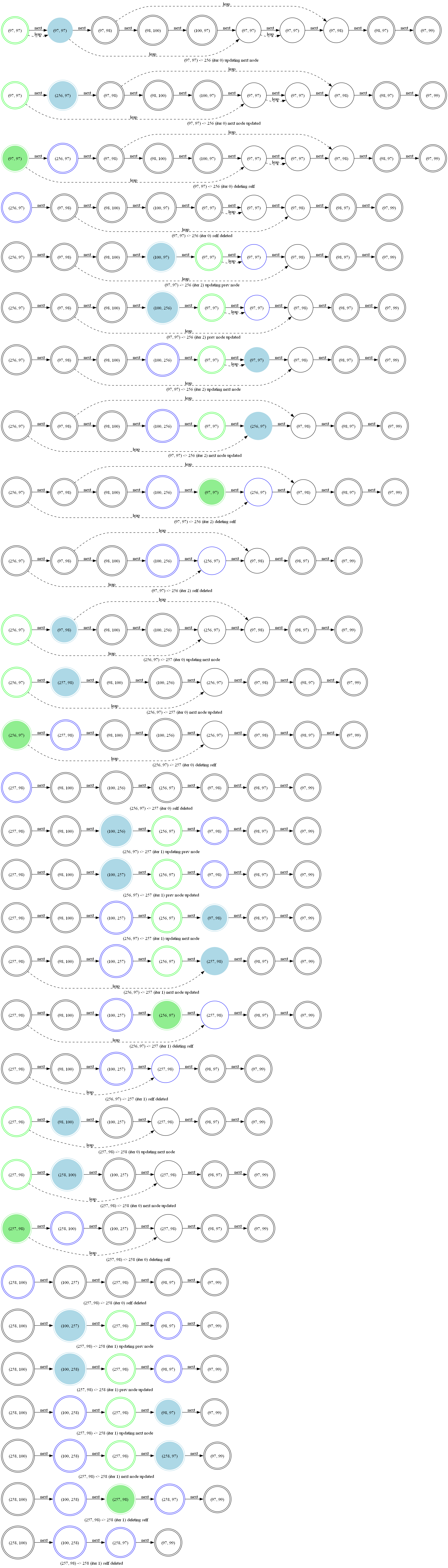
Finally, since the impl with a Leap holding consecutive pairs is more involved, so let’s look at the canonical example from the BPE wiki page of performing 3 merges on the text “aaabdaaabac”. Since the byte pair “aa” (97, 97) is occurring most often, we’ll be merging it first. As our vocabulary starts with 256 tokens, one for each byte, we’ll be performing the merge (97, 97) -> 256.
Here we see that status of the leap right before this merge is performed:
For simplicity I’m only drawing forward edges.
The graph can be interpreted as follows: each node is a circle. Nodes that are first nodes in the leap are double circles. The current node the merge is iterating over is green, while the previous and next nodes are light blue. Finally the node that is just about to be changed (or that was just changed) is filled.
The below illustration (you might want to click on it to zoom!) depicts the status of the leap each time that it changes while performing 3 merges with the above text. The label under each line explains what is going on at that stage:
Hope you enjoyed this post and thanks again Andrej for the fun exercise!