Simple Shader Ray Tracer with Shadertoy

  • Yaniv Leviathan
  • Graphics

I recently discovered Shadertoy which let’s you write pixel shaders in a super convenient way in your browser. It is so easy to use that from discovering it, in a bit over an hour I had a simple ray tracer rendering some lit spheres with the obligatory reflections (thanks Matan Kalman for the inspiration!). This is the end result:

Demo

Let’s deconstruct it and see how it works.

Colors

We’ll have our spheres change color with time. Changing color in a nice way in the RGB domain is hard, because really what we want is to just change the hue (keeping the saturation and value fixed). Luckily the transformation from the HSV space to the RGB space is super simple:

vec3 hsv2rgb(vec3 c) {
  vec4 K = vec4(1.0, 2.0 / 3.0, 1.0 / 3.0, 3.0);
  vec3 p = abs(fract(c.xxx + K.xyz) * 6.0 - K.www);
  return c.z * mix(K.xxx, clamp(p - K.xxx, 0.0, 1.0), c.y);
}

We can keep the Value component fixed at 1.0, and let the Hue and Saturation components range from 0.0 to 1.0 on the X and Y axes respectively with this simple shader:

void mainImage(out vec4 fragColor, in vec2 fragCoord) {    
  vec2 uv = fragCoord / iResolution.xy;
  fragColor = vec4(hsv2rgb(vec3(px.x, px.y, 1.)), 1.);
}

This results in this image:

Whereas fixing the Saturation component at 1.0, and letting the Hue and Value components range from 0.0 to 1.0, results in this image:

Rendering Spheres

The most basic primitive we’ll need is a way to intersect a ray with a sphere. We’ll be representing our rays by a pair of vec3s: r0 denoting the origin of the ray, and rd denoting the ray’s direction (this will be a normalized vector). The sphere will be represented by a vec3 center for its center and a float r for the radius. To get the intersection, we’ll be solving a quadratic equation (Wikipedia has a good explanation):

float raySphereIntersect(vec3 ro, vec3 rd, vec3 center, float r) {
    float a = dot(rd, rd);
    vec3 to_center = center - ro;
    float b = -2.0 * dot(rd, to_center);
    float c = dot(to_center, to_center) - (r * r);
    if (b*b - 4.0*a*c < 0.0) {
        return -1.0;
    }
    return (-b - sqrt((b*b) - 4.0*a*c))/(2.0*a);
}

Let’s add several colored small spheres, that move in a nice way around a larger central sphere:

void intersectScene(vec3 ro, vec3 rd, out bool hit, out vec3 ip, out vec3 norm, out vec3 color) {
	float mn_t = 10000000000.;
  hit = false;
  for (int i = 0; i < NUM_SPHERES + 1; ++i) {
    float f = float(i) / float(NUM_SPHERES);
    #define TWISTS 10.
    float sphere_dist_wiggle = 1.;
    float sphere_dist = 4. + sin(TWO_PI * f * TWISTS + iTime * 3.) * sphere_dist_wiggle;
    float a = f * TWO_PI * 1. + iTime; // angle of rotation around the z axis
    float b = f * TWO_PI * 2. + iTime;
    // c is the center of the sphere.
    vec3 c = vec3(cos(a)*cos(b), sin(a)*cos(b), sin(b));
    c *= sphere_dist;
    float radius = 0.7;
    if (i == NUM_SPHERES) {
      c = vec3(0.);
      radius = 1.5;
    }
    bool c_hit;
    vec3 c_ip;
    vec3 c_norm;
    float t;
    t = raySphereIntersect(ro, rd, c, radius);
    if (t >= 0. && t < mn_t) {
      mn_t = t;
      hit = true;
      ip = ro + rd*t;
      norm = normalize(ip - c);
      float c = abs(f-0.5)/2. + iTime/10.;
      color = hsv2rgb(vec3(c, 1., 1.));
      if (i == NUM_SPHERES) {
        color = vec3(0.7, 0.7, 0.7);
      }
    }
  }
}

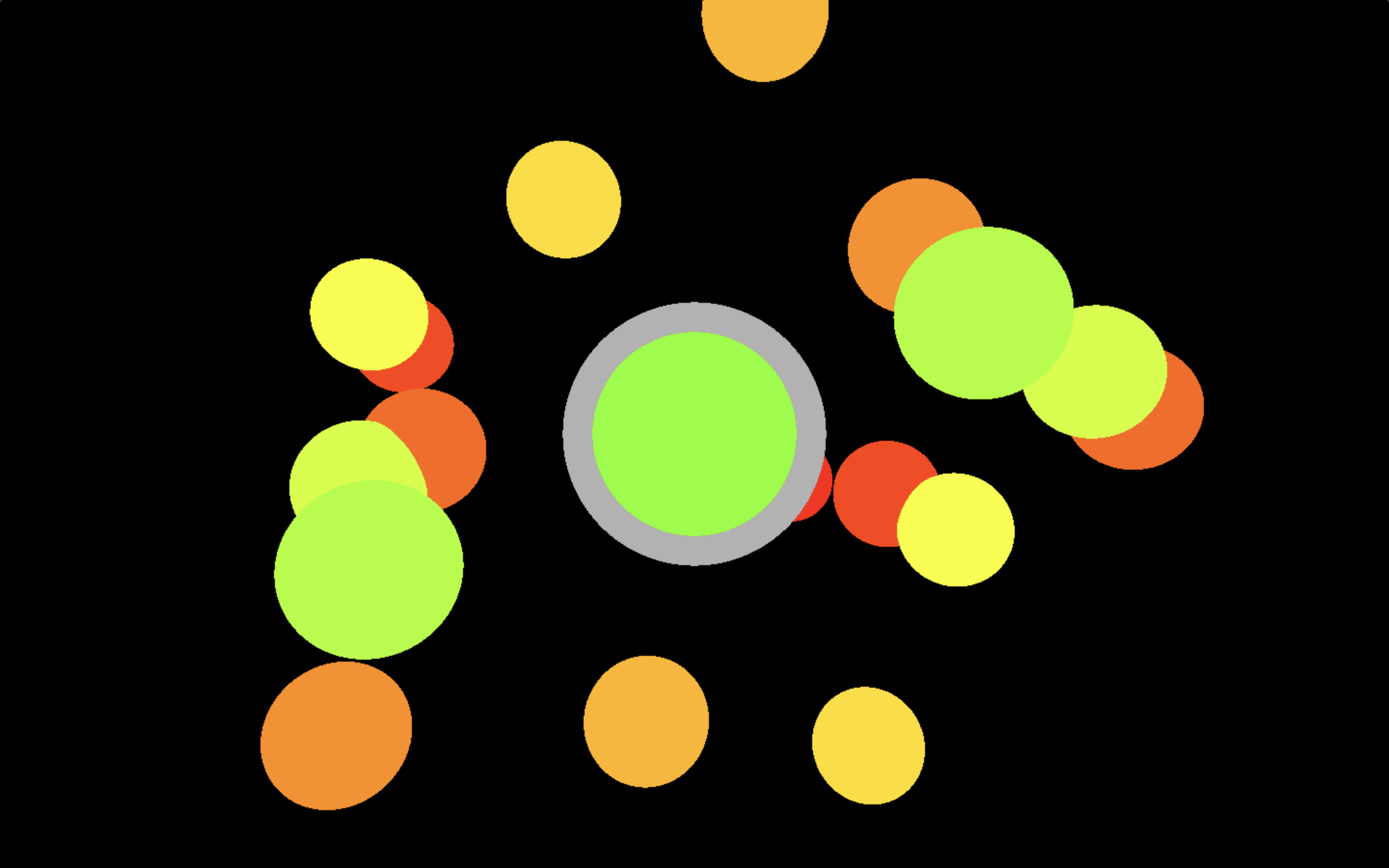
Without further lightning, this looks like this:

Let There Be Light

To get the spheres lit, we will need the ray’s direction (rd), the intersection point (p), the sphere’s normal at the intersection point (norm) and the sphere’s color (c).

We will first calculate a sphere’s color at a point, without reflections:

\[Light = Ambient + Diffuse + Specular\] 
vec3 light(vec3 rd, vec3 p, vec3 norm, vec3 c) {
  vec3 ambient = c * LIGHT_AMBIENT_COLOR;
  float d = dot(norm, normalize(LIGHT_POS - p));
  vec3 diffuse = clamp(d, 0., 1.) * LIGHT_COLOR * c;
  vec3 specular = vec3(0.);
  if (d > 0.) {
    float x = max(0.0, dot(reflect(normalize(lightPos-p), norm), rd));
		float specular_strength = pow(x, 200.);
    specular = vec3(specular_strength);
  }
  return ambient + diffuse + specular;
}

And then recurse over the scene, spawning a new reflected ray every time we intersect one of the spheres:

vec3 render(inout vec3 ro, inout vec3 rd) {
  vec3 col = vec3(0.);
  float alpha = 1.;
  for (int i = 0; i < REFLECTION_DEPTH; i++) {
    bool hit;
    vec3 norm;
    vec3 p;
    vec3 c;
    intersectScene(ro, rd, hit, p, norm, c);
    if (!hit) {
      break;
    }
    col += light(rd, p, norm, c) * alpha;
    alpha *= 0.4;
    rd = reflect(rd, norm);
    ro = p + 0.01*rd;
  }
  return col;
}

Putting it all together we get this:

Share this story