This is the second post in the Straight-Edge and Compass series (make sure you have read the first part here before continuing).

We are now ready to define the rules for our second, more complex game - “Construction with a Straight-Edge and a Compass“. These are very similar to the rules of “Constructions with a Straight-Edge Only” (defined in the previous post) except that now, in addition to creating infinite straight lines, you can also create circles, as follows: given 2 points, a and b, you can create the circle with center at a that passes through b. A point is added to the set of points if it is the intersection of 2 lines (as before), of two circles, or of a circle and a line.

Now, the addition of the new tool (the compass) enables us to construct many more points than before. If the initial set of points contains only one point then, as before, no new points can be constructed. But if the initial set of points contains two points, then the set of constructable points is infinite (we will shortly prove it). The subject for this second part of the topic will be analysing the set of constructable points in our new game.

Note that it is enough to examine the constructable-points’ set, P, from the initial set A = {(0, 0), (1, 0)}. This is because if the initial set of points contains other two points, a and b (instead of (0,0) and (1,0)), then there is an affine operator M acting on the euclidean-plane and consisting of translations and rotations, such that a becomes the origin and b becomes (1,0). Denote the inverse of M by N (of course M is reversible as long as a and b are different). Then the set of points constructable from the initial set {a, b} is the same as the set N(P).

So our question is, “what points belong to P, the set of constructable points, from the initial set A = {(0, 0), (1, 0)}?”

Developing Basic Tools

In order to answer this question we shall develop some tools.

Mid-Point Perpendicular

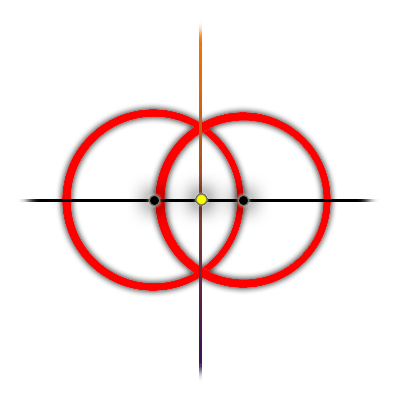
Given two points, a and b, we can construct the line passing through their mid-point that is perpendicular to the line passing through a and b. This is done as depicted here (the yellow dot is the constructed mid-point):

Point Reflection

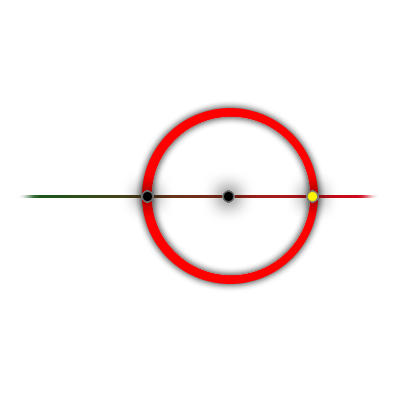
Given a point a and a point b, we can create the point c (that is different from a) lying on the line through a and b and whose distance from b is the same as the distance from b to a. This can be done by using the straight-edge to create the line through a and b and then use the compass with center at b and leg at a. c is the intersection of this circle and line:

Creation of the Axis

The x-axis is easily constructable from the two initial points by using the straight-edge. The point (-1, 0) is constructable from the initial points by using Point Reflection. The y-axis is then constructable from (-1, 0) and (1, 0) by using Mid-Point Perpendicular.

Axis Flip

Given a point on the x-axis of the form (a, 0), create the point (0, a) on the y-axis, and vice versa. Given the Creation of the Axis, as above, performing an Axis Flip is very easy.

Coordinate Selection

Exercise for the reader: given a point (x, y) create the point (x, 0).

Constructable Numbers and Distances

Constructable Numbers

Now we shall note that the notion of constructable points in our new game can be changed a bit to the notion of constructable numbers. A number x is constructable if the point (x, 0) is constructable. Note that if a point (x, y) is constructable, then both x and y are constructable (by using Axis-Flip and Coordinate-Selection). If on the other hand x and y are constructable numbers, then again by using Axis Flip we get that (x, 0) and (0, y) are constructable points. By using a trick similar to what we did for creating the y-axis, the point (x, y) is shown to be constructable. So we shall now only consider the simpler notion of constructable numbers instead of constructable points.

Constructable Distances

We have shown a relation between constructable points and constructable numbers. We can also consider the notion of constructable distances. A number d is a constructable distance, if it is the distance between two constructable points. It can be shown that a number d is a constructable number i.f.f. (if and only if) d is a constructable distance. One direction is easy. Can you prove the other?

More Tools

Lets continue to build our tools, this time for constructable numbers.

The Integers

All the integers are constructable numbers. 0 and 1 are constructable (as (0,0) and (1, 0) are in the initial set). Given the integers i and and i-1 integer i+1 can be constructed. Just place the compass’ center on the point (0, i) and its leg on (0, i-1) and the circle’s intersection with the x-axis yields i+1. Integer i-2 can be constructed in a similar fashion. By induction all integers (positive and negative) are constructable.

Negation

If x is constructable then -x is constructable. This is obvious (can you see why?).

Addition and Subtraction

Given constructable numbers a and b, a+b is a constructable number. We can construct -b, and so a+b is a constructable distance. Using the equivalence stated above (which I have left as an exercise to the reader) between constructable distances and constructable numbers, a+b is constructable. Addition and Negation lead to Subtraction.

Multiplication and Division

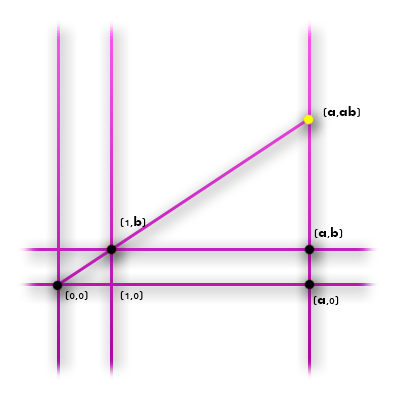
If a and b are constructable numbers, so are \(a \times b\) and \(\frac{a}{b}\). The construction for multiplication is depicted below (division is similar):

We have just proved an important theorem: the rational numbers \(\mathbb{Q}\) are constructable \(\blacksquare\)

Actually, we have reached a more important conclusion: the constructable numbers constitute an extention field of \(\mathbb{Q}\), the field of rational numbers.

We are getting closer to the answer we are looking for, as we already know quite a bit about the set P of constructable points.

To be continued…