I am taking a course about Hilbert Spaces this semester. A very basic notion in a Hilbert Space is that of the norm. For a while now, I kept several questions regarding norms in the back of my mind, and as I finally got to think about them, I wanted to share my conclusions with you.

Introductory Concepts

Let’s start from the beginning (those of you familiar with Normed Spaces can skip this section). A linear space is a set of objects with two operations:

1. Addition (marked by the symbol +) which acts on two elements of the space and returns an element of the space.
2. Multiplication (marked by the symbol ×) which acts on an element of the space and a real number and returns an element of the space.

The operations must follow these rules (x and y are elements of a linear space, a and b are real numbers):

1. x + y = y + x (+ commutativity)
2. x + (y + z) = (x + y) + z (+ associativity)
3. Existence of a zero element (marked by the symbol 0) such that for every element of the space: 0 + x = x + 0 = x
4. For every element x of the space, existence of a negative element (marked by -x) such that: -x + x = 0
5. (a × b) × x = a × (b × x) (× associativity)
6. For every element x of the space, 1 × x = x
7. a × (x + y) = a × x + a × y (distributive law 1)
8. (a + b) × x = a × x + b × x (distributive law 2)

A simple example of a linear space is the Euclidean space of n dimensions (for any n ≥ 1).

Note that we define the minus symbol, -, as follows:

x – y = x + (-1 × y)

Now, a norm is essentially a function that somehow tells us how far away an element of our space is from the neutral element (0).

We write ‖x‖ for the norm of x.

The norm can also tell us how far apart two elements of the space are. We say that the norm generates a distance. This is done as follows:

dist(x, y) = ‖x – y‖

Formally, a norm is a function from the linear space to \(\mathbb{R}+\) (the set of non-negative real numbers), such that (x and y are elements of the linear space, a is a real number):

1. ‖a × x‖ = |a| × ‖x‖ (homogeneity)
2. ‖x + y‖ ≤ ‖x‖ + ‖y‖ (triangle inequality)
3. ‖x‖ ≥ 0 and ‖x‖ = 0 i.f.f. x = 0

Examples

Now let’s consider the 2-dimensional euclidean plane as our linear space (call it \(\mathbb{R}_2\)). An example of a norm in \(\mathbb{R}_2\) is the euclidean norm (where u=(x,y) is a member of \(\mathbb{R}_2\)):

\[\lVert u \rVert = \sqrt{x^2 + y^2}\]

We shall call this norm, the \(l_2\) norm.

For those of you not familiar with the concept of the norm, verifying that this is indeed a norm may prove insightful.

The \(l_2\) norm is very useful as it measures actual distances in a plane.

Now let’s consider another norm, called the \(l_1\) norm:

‖u‖ = |x| + |y|

Again, it can be easily verified that this is indeed a norm. This norm obviously generates a different distance than that of the plane. Does it have a “real-world” use? You are encouraged to take a minute of reflection upon this before reading on…

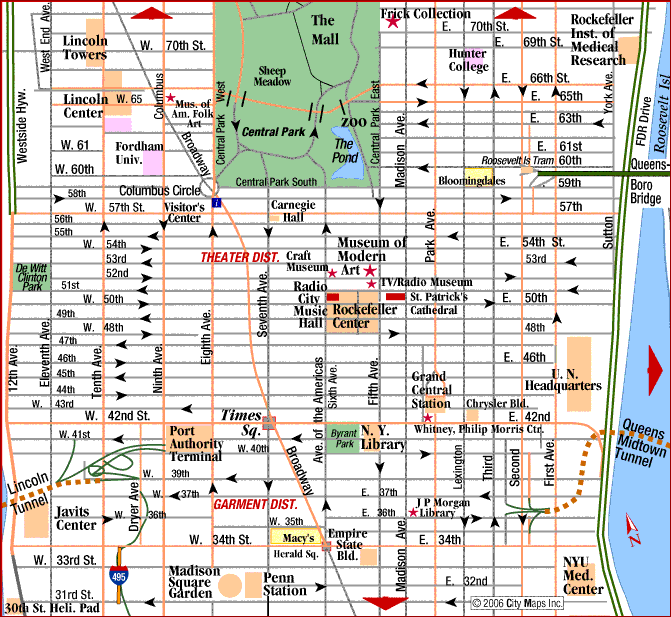
Well, yes, it does have a use. Let’s say that we are standing in Midtown-Manhattan.

What is the distance between us? The aerial distance is the regular euclidean distance (neglecting the roundness of the Earth) but the walking distance is the distance generated by the \(l_1\) norm! This is caused by the fact that we can only walk along the streets (i.e. parallel to the axes!). For this reason the distance generated by the \(l_1\) norm is sometimes referred to as the Manhattan-Distance.

Now, let’s consider a third norm called \(l_\infty\), defined as:

‖u‖ = max(|x|,|y|)

Again, this is obviously a norm (check it!).

Now let’s start with the fun stuff…

First, can you figure out the meaning of the names of the norms (\(l_1, l_2, l_\infty\))?

For all p ≥ 1, let’s define the function \(f_p:\mathbb{R}_2 \rightarrow \mathbb{R}+\) as:

\[f_p(u) = (x^p + y^p)^{\frac{1}{p}}\]

Then \(f_p\) is a norm on \(\mathbb{R}_2\) and we call it \(l_p\) (I feel like I am repeating myself, but again, this can be easily checked).

The names of \(l_1\) and \(l_2\) become obvious right away, and so does the name of \(l_\infty\) (after a little thought :-) ).

If you still can’t figure it out: \(l_\infty(x)\) is the point-wise limit of \(l_p(x)\) as \(p \rightarrow \infty\) for all the elements x of \(\mathbb{R}_2\). Actually, the functions \(l_p\) converge to \(l_\infty\) locally-uniformly (can you prove this?).

This brings up an interesting question: Do norms other than \(l_1\) and \(l_2\) have any “real-world” meaning? If you have any insights on this, please comment!

Unit Circles

The unit circle of a normed space is the subset of elements of the space such that their norm is equal to 1.

Can you figure out how \(l_1\), \(l_2\) and \(l_\infty\) unit circles look like in \(\mathbb{R}_2\)?

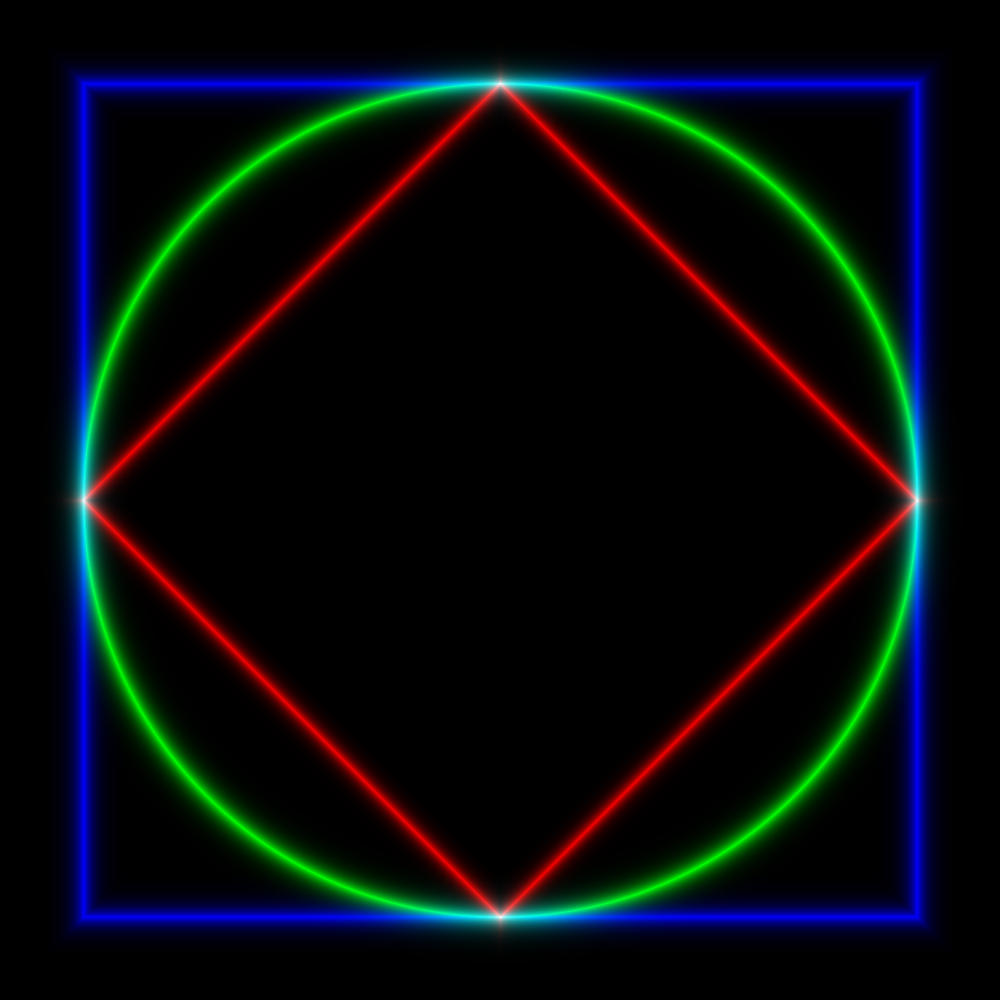
As I found it difficult to visualize the unit circles for norms \(l_p\), p > 2, I jotted down a few lines of C in order to create the following images:

The red, green, and blue shapes denote the unit circles for the \(l_1\), \(l_2\), and \(l_\infty\) norms respectively.

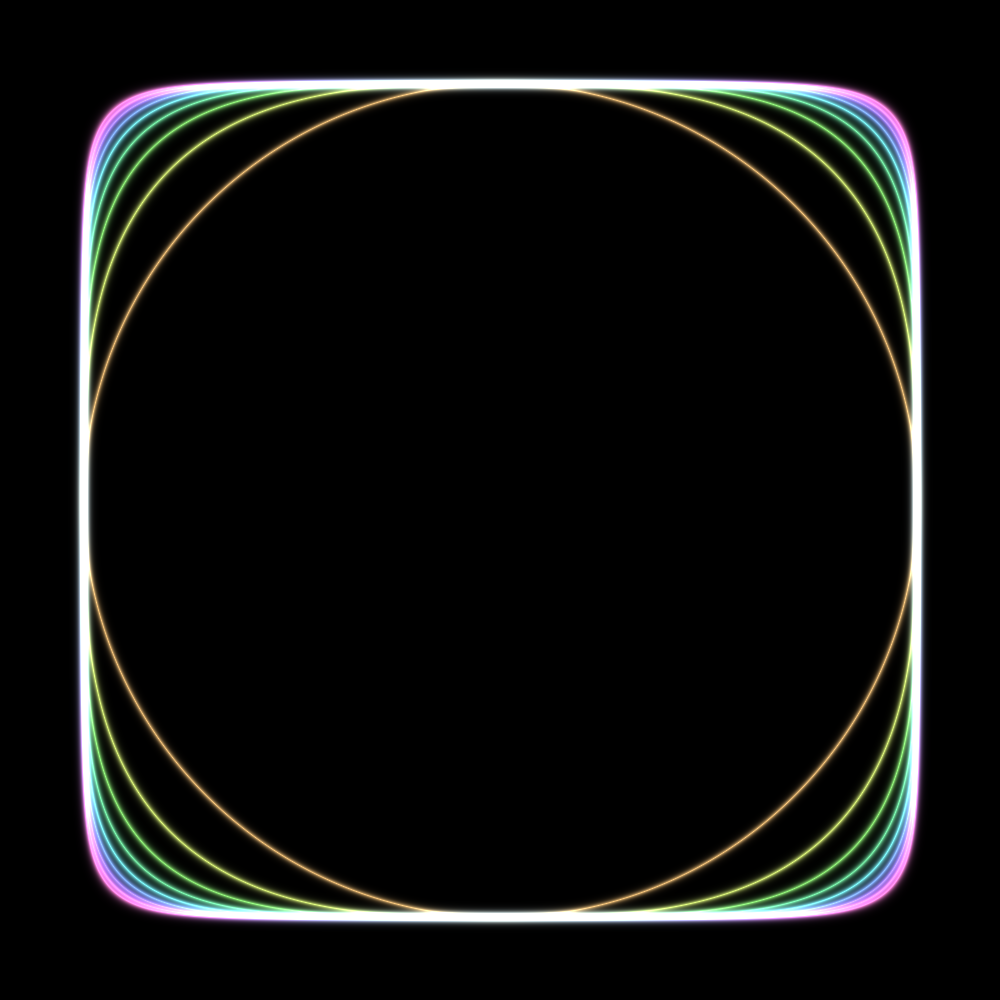
Here’s another drawing showing the unit circles for \(l_p\) norms for various values of \(p \ge 2\):

In the picture I included values of p that are not whole numbers. This should not pose any problems.

Finally, in this picture I also included values of p that are less than 1 (the shapes inside the \(l_1\) circle). These are there for illustration purposes only, as they do not constitute norms:

Note: the glowing effect was generated by my program to overcome jagged edges caused by precision issues.

Something else to think about is the volume of the unit circles. The volume of the unit circle under the \(l_1\) norm is 2, under the \(l_2\) norm is Π and under the \(l_\infty\) norm, 4.

Can you supply some more values?

Visualizing the Norms

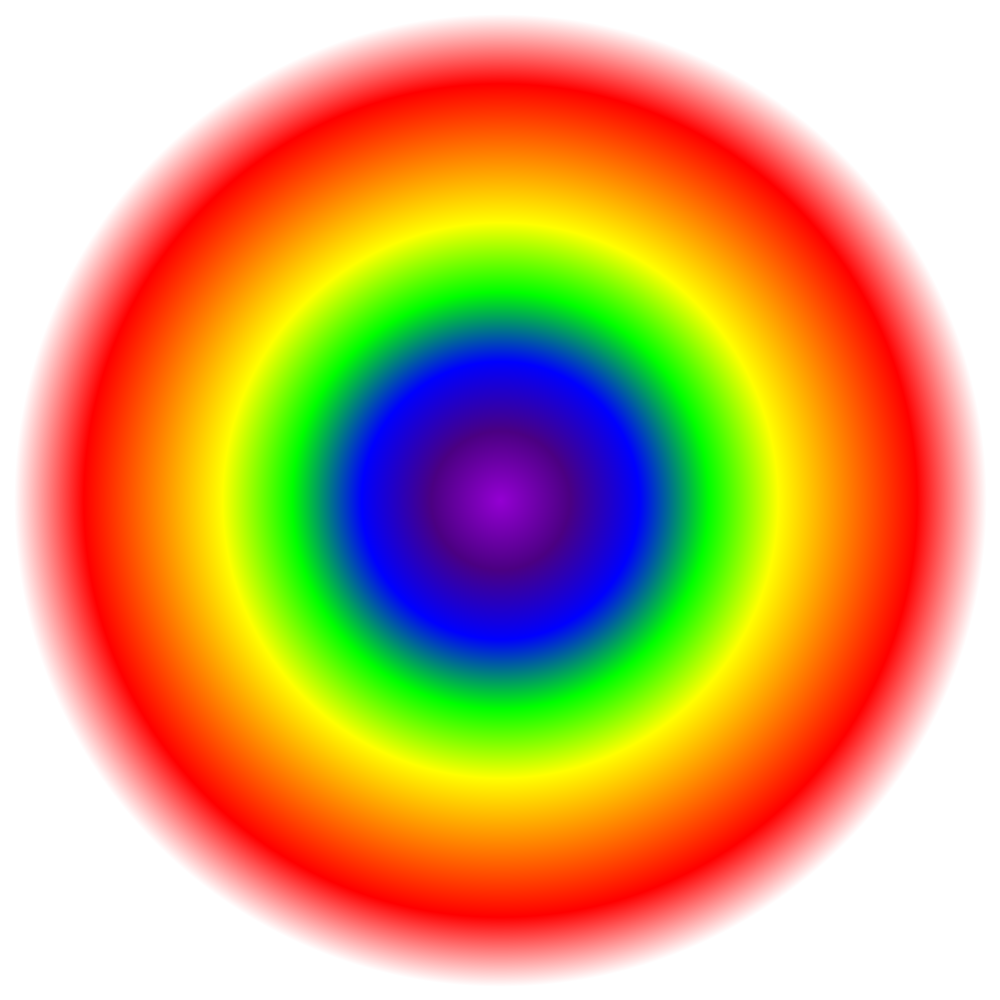
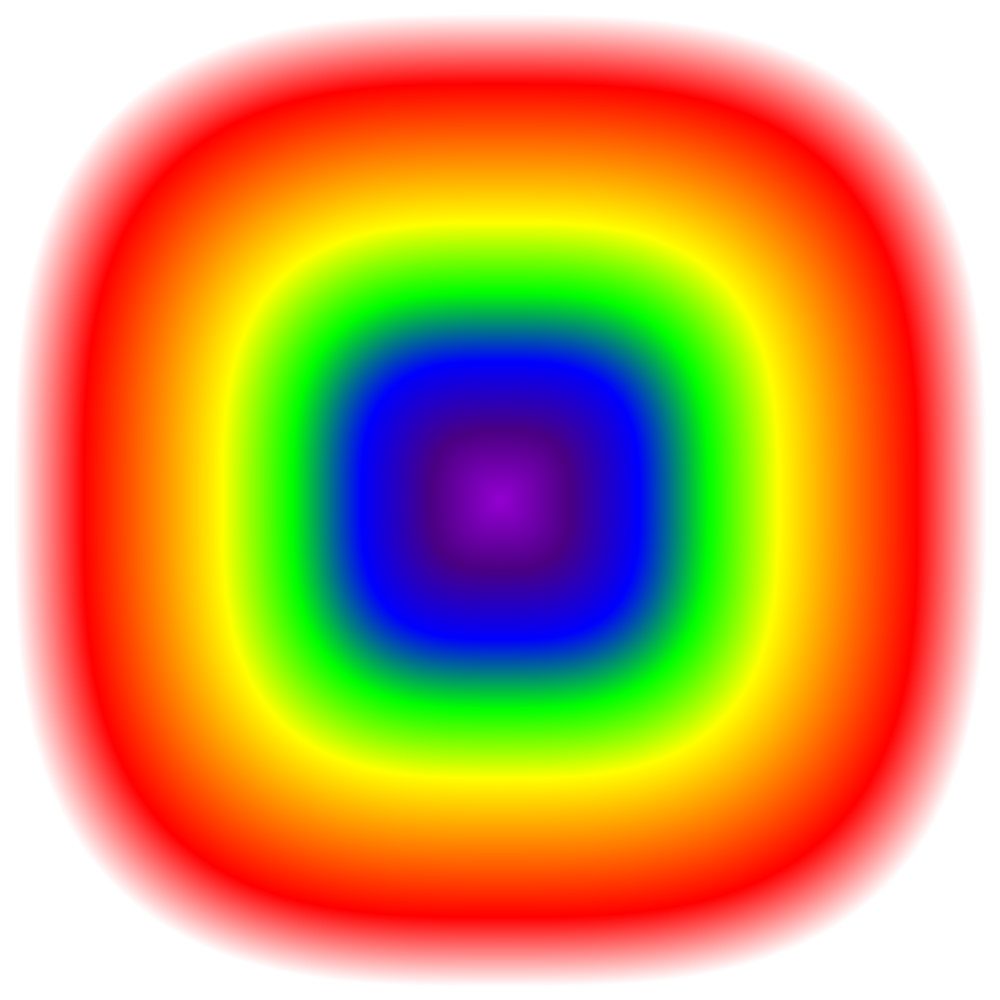
While the unit circles above are very informative, I wanted to see how the norms look like in the entire plane. I therefore plotted the \(l_1\), \(l_2\), \(l_3\), and \(l_\infty\) norms in the entire plane, using this scale:

So purple is 0, and red is 1. This is the \(l_1\) norm:

This is the \(l_2\) norm:

This is the \(l_3\) norm:

And finally, this is the \(l_\infty\) norm:

That’s it for now!

I might update this article, so check the updates section!