Consider an infinite checkerboard divided in two with an infinite line lying along the x-axis, as depicted below:

Let’s zoom in a little:

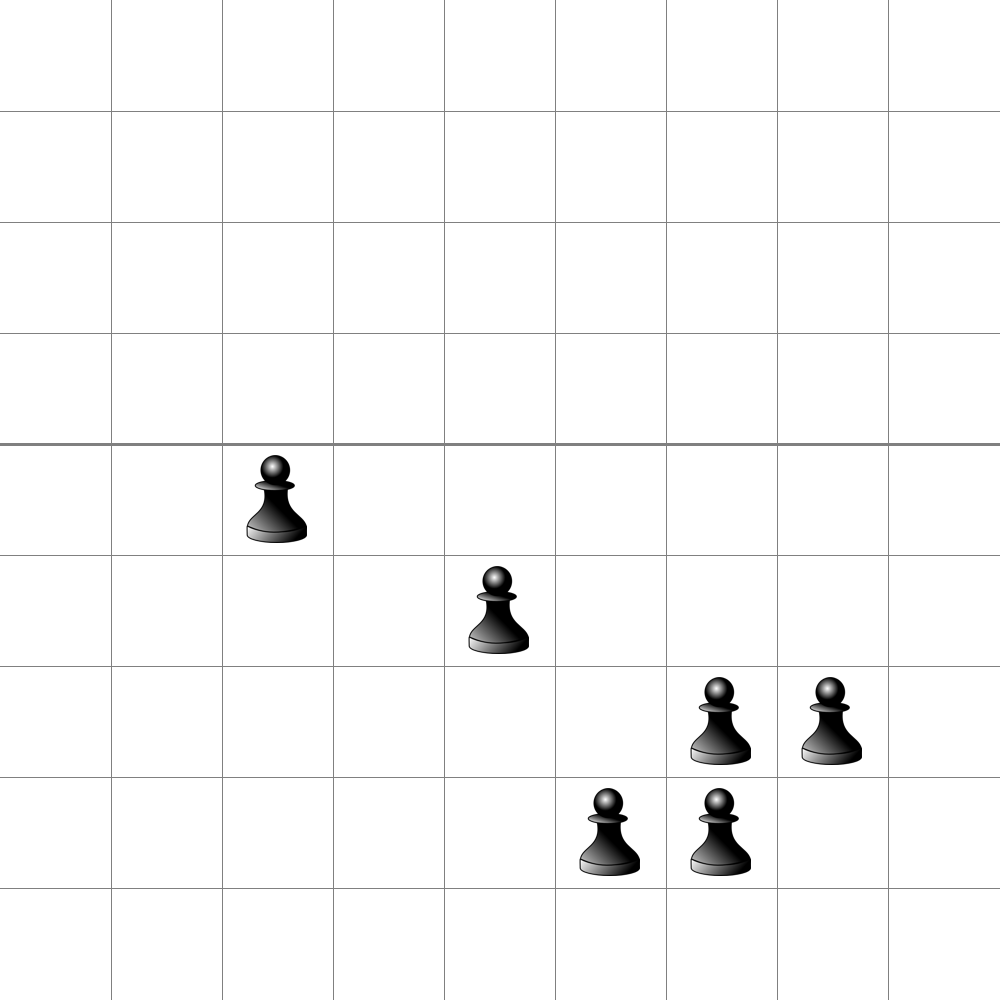
We will play a game on this board. In this game, you start with some pawns under the horizontal line. For example, here is a potential starting configuration:

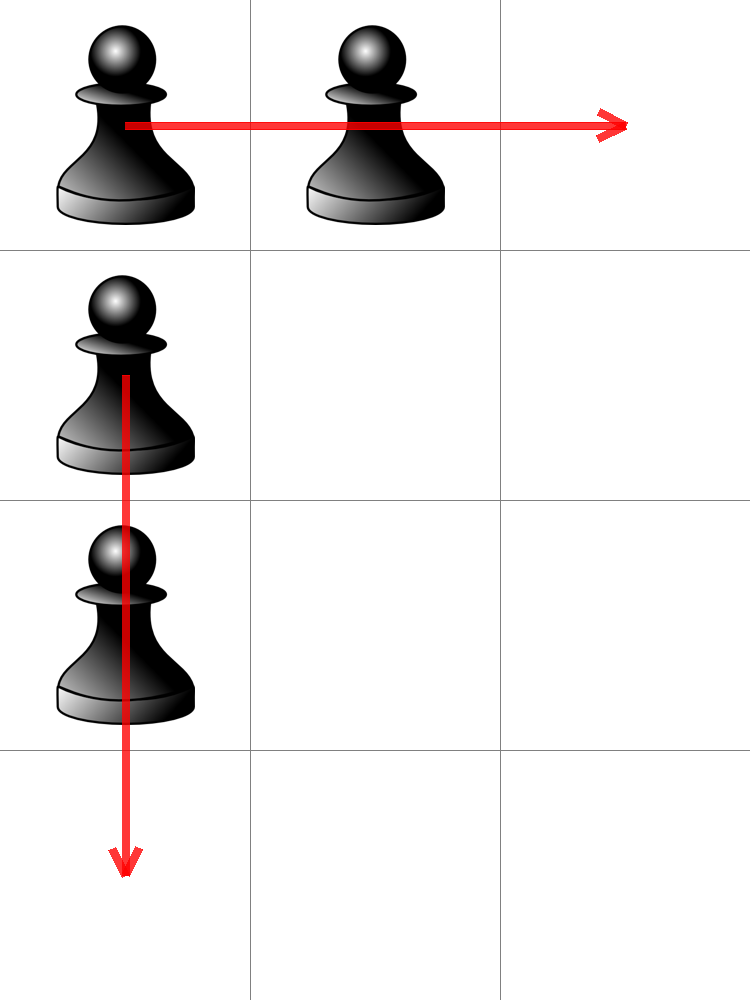
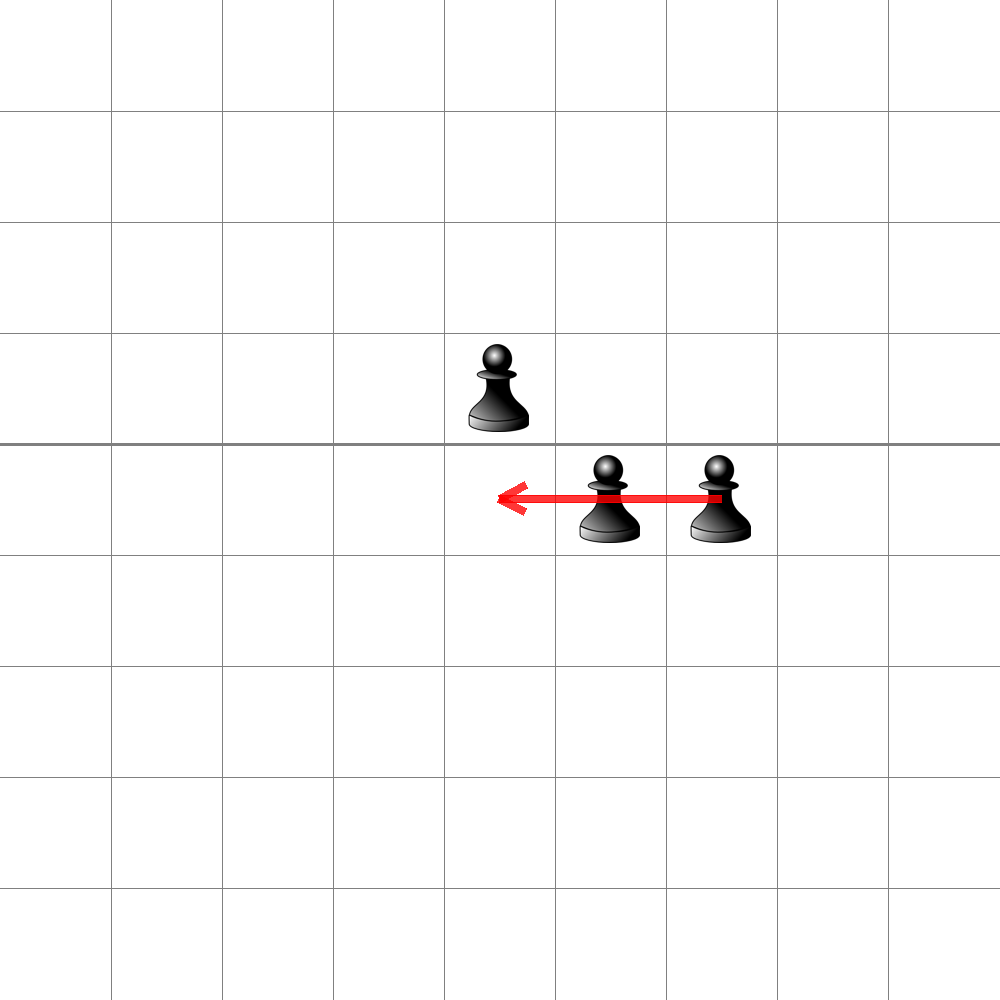
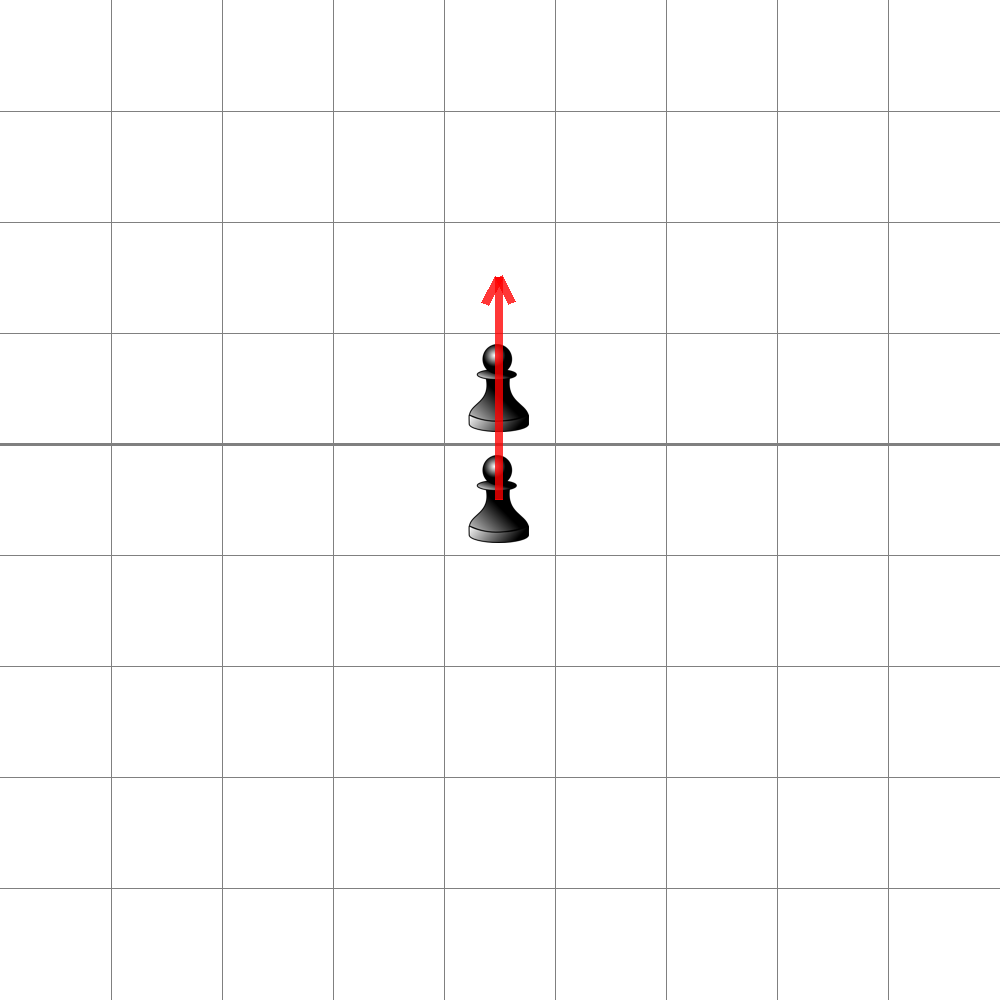
In each turn you can make a pawn jump over one of its 4-connected neighbors, thereby killing it (removing it from the board). The pawn’s movement is demonstrated here:

Will become this:

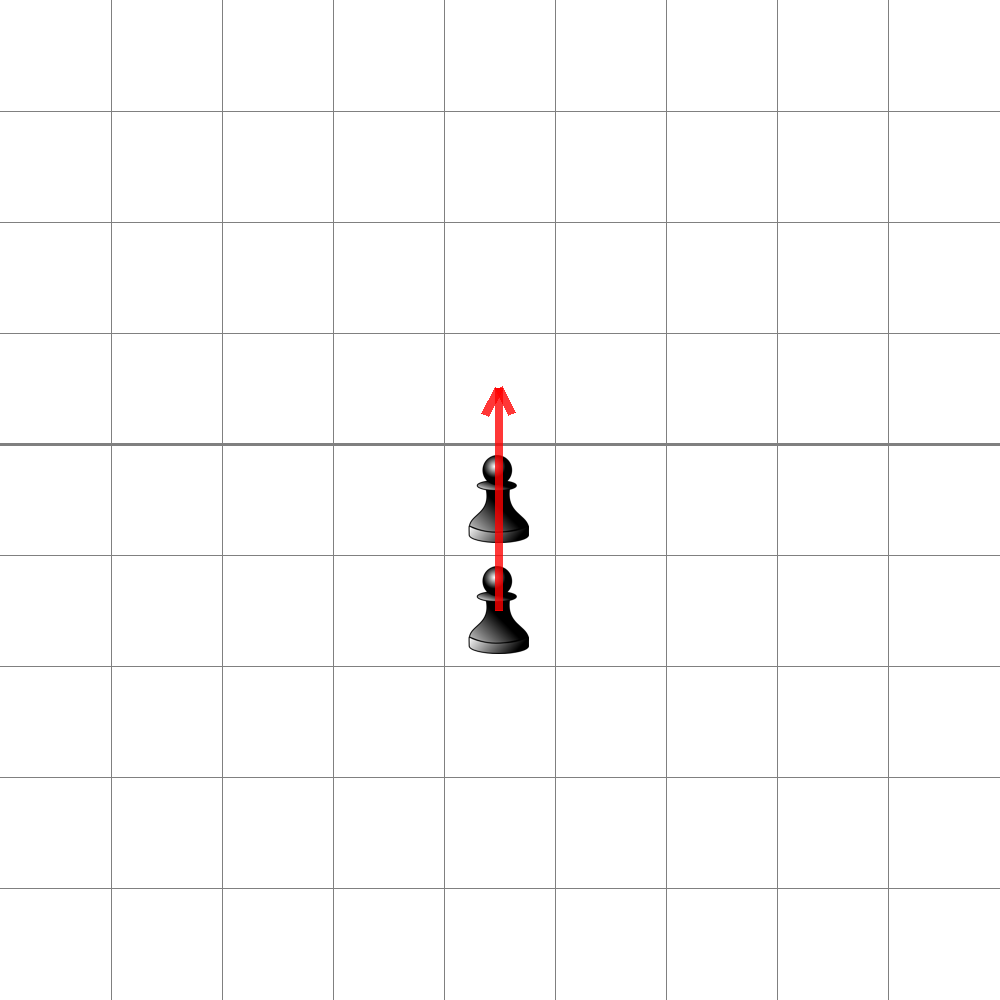
When the game starts, all the pawns are below the line. You can move the pawns as per the rules above, and you get points depending on how far above the line you can go. For example, here is a starting configuration with 2 pawns and the first move:

Resulting in a game ending with 1 point:

It is obvious that in order to make a pawn cross the line (or move at all), at least two pawns are needed, so all games with a single pawn will end in a score of zero.

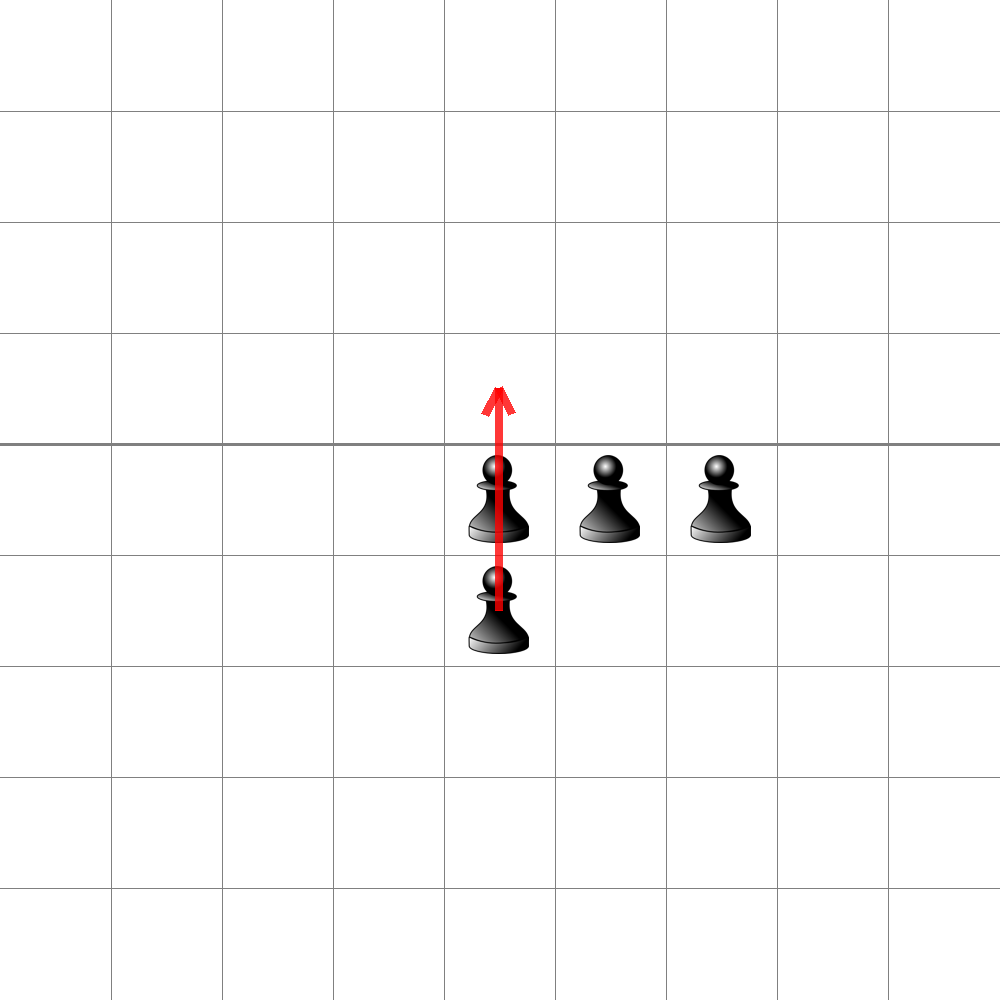
How many pawns are needed in order to score 2 points? As is demonstrated below, 4 pawns are sufficient, and indeed this is the minimum (check that you see why 2 and 3 pawns cannot do it).

Now for the riddle. How many pawns are needed in order to score 5 points?