A short introduction to Graph Theory is needed for this one. If you already are familiar with Graph Theoretic constructs feel free to skip it.

Short Intro to Graph Theory

A graph G, is a pair (V,E) where V is a set of vertices and E is a set of edges. Each edge is an unordered pair of the form (u, v) where u and v are vertices (i.e. they belong to V). The degree of a vertex t (denoted deg(t)) is the number of edges containing it:

\[deg(t) = |\{ e \in E | e = (t, s) \}|\]

In this post I only consider finite and simple graphs. A finite graph is a graph whose vertex-set V is finite. A simple graph is a graph in which there are no loops (i.e. edges of the form (u, u)) and no multiple edges (i.e. E is a proper set so it cannot contain the same element twice).

The following is a trivial claim:

The sum of the degrees in a graph equals twice the number of edges.

It is trivial to prove this claim by induction on the number of edges (on a graph with no edges it is clear, and by adding an edge to the edge set of the graph the sum of degrees increases by two \(\blacksquare\)).

The Riddle

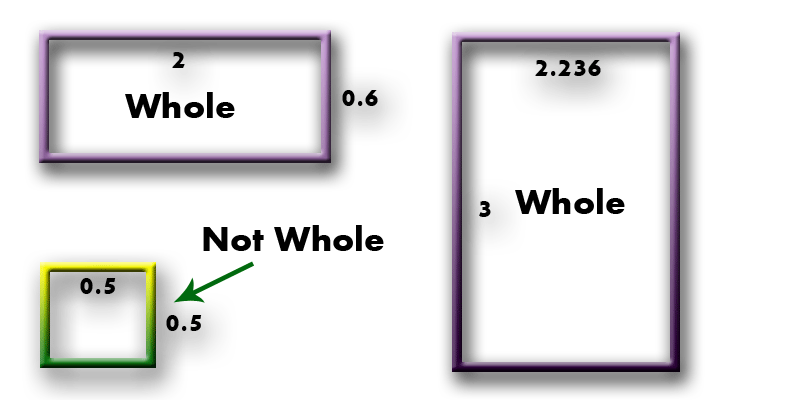
A rectangle is called whole if at least one of its sides is an integer. For example, a rectangle of 2 by \(\frac{3}{5}\) is whole as well as a rectangle of \(\sqrt{5}\) by 3. A rectangle of \(\frac{1}{2}\) by \(\frac{1}{2}\) is not whole. Examples:

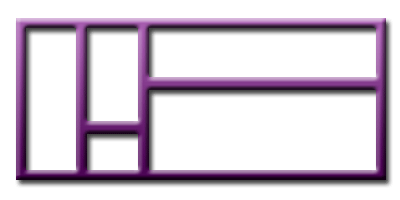
A set T of rectangles constitues a tiling of a rectangle R if the rectangles in T are disjoint and for every point p in R there is a rectangle S in T such that p belongs to S. Example:

Prove that if R is a rectangle and T is a tiling of R consisting only of whole rectangles (i.e. every rectangle S in T is whole) then R is whole.