This puzzle is beautiful, and although its solution is a bit lengthier than usual, it’s definitely worth the effort.

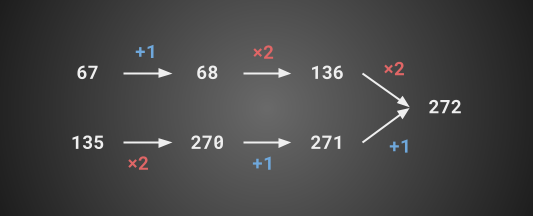
Two integers $a$ and $b$ are $(\times 2, +1)$-equivalent if you can multiply one of them by 2 and add 1 to the other, a finite number of times, and end up with the same number. For example, 67 and 135 are $(\times 2, +1)$-equivalent, as $((67+1){\times}2){\times}2 = ((135{\times}2)+1)+1$:

Are any two integers $(\times 2, +1)$-equivalent?

Thanks to Raya Leviathan (my amazing genius mother) for this riddle!