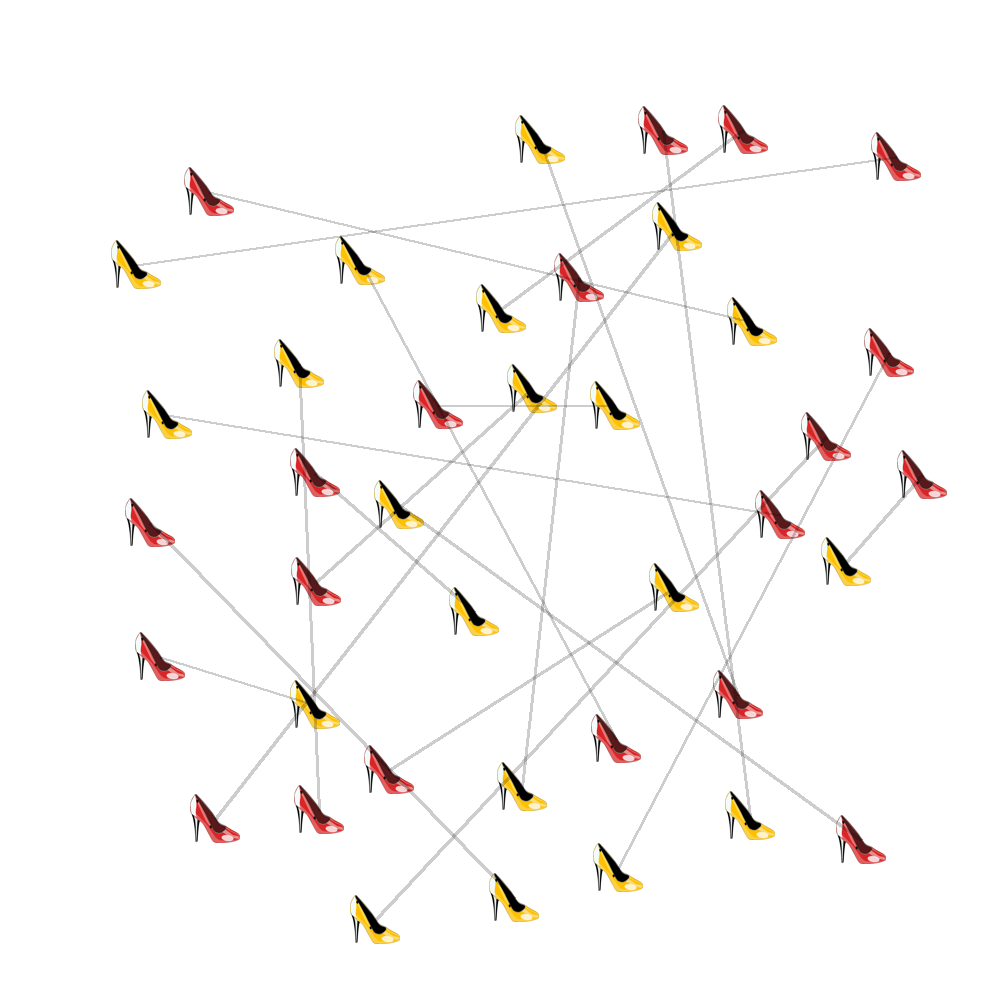
There are 100 red points and 100 yellow points on the plane, such that no three points are on the same line.

A pairing of the points is a one-to-one function that assigns one yellow dot to each red dot.

A valid planar pairing is a pairing such that when paired points are connected with a straight line segment, no line intersections occur.

Prove that there exists a valid planar pairing.

Thanks to Nadav Sherman for giving me this one.

Extra Credit

Is the claim true in the case that the sets of red and yellow points are infinite?

Solution

We will not just prove that a pairing exists, but in fact, devise an algorithm to construct it.

Start by assigning a pairing randomly:

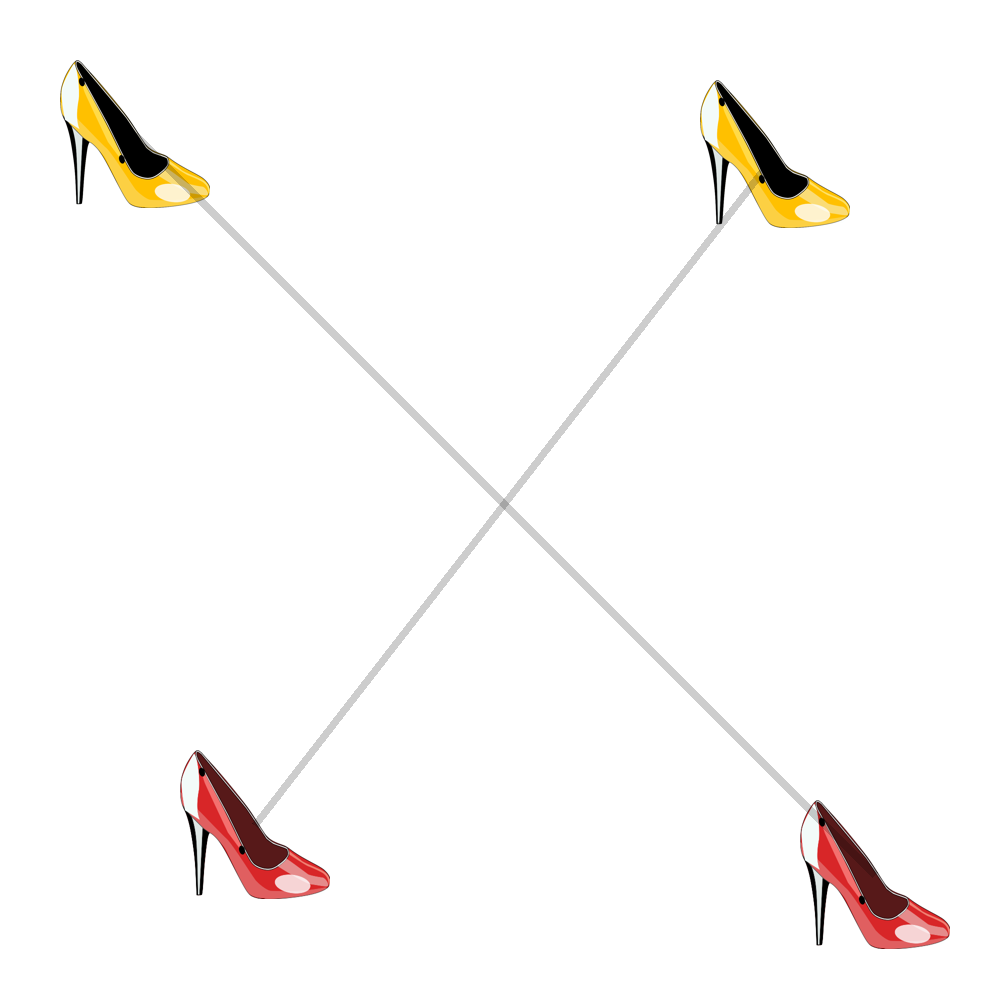
If the pairing is valid, we are done. Otherwise, there exist 2 pairings such that their line segments intersect:

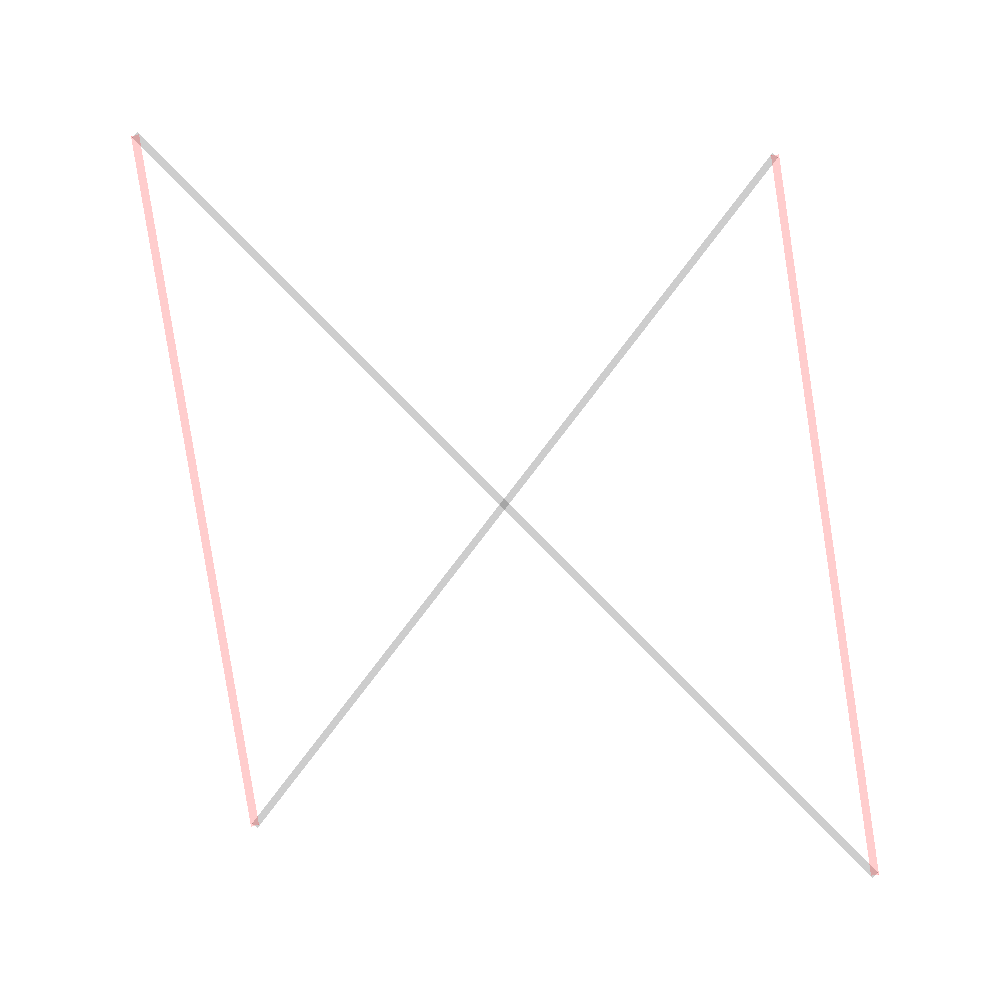
Note that they could intersect with other line segments too, that’s fine. Then simply uncross them, by flipping the pairing function between them:

Again, note that this might result in new intersections - that’s ok, as this process must end after a finite number of steps, thus generating a valid pairing. Why? Well look at the sum of the lengths of all the line segments. After every time we uncross a pair, this sum strictly goes down. That is because due to the triangle inequality, the sum of the lengths of the red lines is strictly less than the sum of the length of the grey lines (remember that the points are not colinear):

Therefore this process must end and a valid pairing exists. \(\blacksquare\)